John Schulman & Thinking Machines : LoRA sans regret LoRA remplace chaque matrice de poids W du modèle original par une version modifiée W’=W+γBAW’=W+γBA, où B et A sont des matrices qui, ensemble, ont beaucoup moins de paramètres que W. LoRA fonctionne de manière similaire à un ajustement complet lorsque : 1. LoRA est appliqué à toutes les couches du réseau, en particulier les couches MLP/MoE qui contiennent la plupart des paramètres. 2. LoRA n'est pas contraint par sa capacité, c'est-à-dire que le nombre de paramètres entraînables dépasse la quantité d'informations à apprendre, ce qui peut être estimé en termes de taille de jeu de données. Implications : De grands modèles de base (par exemple, des modèles de trillion de paramètres) peuvent être personnalisés à une fraction du coût de l'entraînement d'un nouveau modèle.

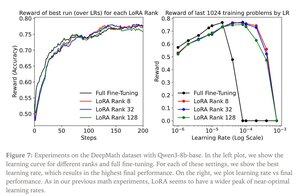
Publication de Thinking Machines : Gemini sur les exigences de calcul pour LoRA sur un modèle de pointe - toujours redoutable, mais le nombre de paramètres utilisés est inférieur à 1 % de la taille totale du modèle (pré-entraînement).