John Schulman y Máquinas Pensantes: LoRA Sin Pesar LoRA reemplaza cada matriz de peso W del modelo original con una versión modificada W'=W+γBAW'=W+γBA, donde B y A son matrices que juntas tienen muchos menos parámetros que W. LoRA funciona de manera similar al ajuste completo cuando: 1. LoRA se aplica a todas las capas de la red, especialmente a las capas MLP/MoE que albergan la mayoría de los parámetros. 2. LoRA no tiene limitaciones de capacidad, es decir, el número de parámetros entrenables excede la cantidad de información que se debe aprender, que se puede estimar en términos de tamaño del conjunto de datos. Implicaciones: Los modelos base grandes (por ejemplo, billones de parámetros) se pueden personalizar a una fracción del costo de entrenar un nuevo modelo.

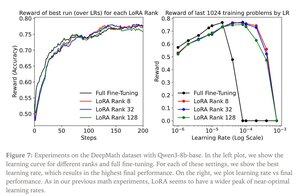
Publicación de Thinking Machines: Gemini sobre los requisitos de cómputo para LoRA en un modelo de frontera: sigue siendo formidable, pero el número de parámetros utilizados es inferior al 1% del tamaño total del modelo (preentrenamiento).